exupero's blog
RSSApps

Improving generated Lindenmeyer rules

In the previous post I randomly generated some Lindenmeyer systems, but only about a third of seeds I tried generating something other than a line or squares. Others were somewhat chaotic, without the pleasing regularity we like to see in fractals. Rather than generating L-system definitions purely randomly, let's see if there are higher-order patterns in attractive systems.

One idea is to look at how steps follow each other in expansion rules. Here's a function to collect that info from an L-system rule:

(defn successors [rule]
  {:start (first rule)
   :successors (reduce
                 (fn [res [a b]]
                   (update res a (fnil conj []) b))
                 {}
                 (partition 2 1 rule))})

Let's check for higher-order patterns in the simpler of the L-systems we've seen so far, the Koch snowflake and Koch curve:

(koch-snowflake :rules)
{F [F + F - - F + F]}

(successors (get (koch-snowflake :rules) 'F))
{:start F, :successors {F [+ - +], + [F F], - [- F]}}

(koch-curve :rules)
{F [F + F - F - F F + F + F - F]}

(successors (get (koch-curve :rules) 'F))
{:start F, :successors {F [+ - - F + + -], + [F F F], - [F F F]}}

The symmetry of the original rules does seem to show up, possibly in a way we can generate. The successors of + and - are brief sequences of mostly F, while the sequence of successors of F suggests a mirror pattern, in which the end of the sequence either mirrors the beginning, or it mirrors the beginning and inverts the turns. Here are two functions to do just that:

(defn mirror [steps]
  (concat steps (rest (reverse steps))))
(defn mirror-and-invert [steps]
  (concat steps (map #(get '{+ -, - +} % %) (rest (reverse steps)))))

To keep generated sequences from terminating prematurely, we'll generate a successor for each + and - in the successors of F:

(defn successors-length [steps step]
  (count (filter #{step} steps)))

Now we can generate successors:

(defn generate-successors [rng]
  (let [successors-f (repeatedly (rng-rand-int rng 3 5) #(rng-rand-nth rng '[F + -]))
        op (rng-rand-nth rng [mirror mirror-and-invert])
        f (op successors-f)]
    {:start 'F
     :successors {'F f
                  '- (repeatedly (successors-length f '-)
                                 #(rng-rand-nth rng '[F F F -]))
                  '+ (repeatedly (successors-length f '+)
                                 #(rng-rand-nth rng '[F F F +]))}}))

A couple things to notice: first, experimentation suggests favoring F to follow + and -; secondly, it's not very fruitful to follow + with - or vice versa.

To draw a generated system, we'll need to convert this "successors encoding" into an L-system definition:

(defn successors->rule [{:keys [start successors]}]
  (loop [step start
         expansion [start]
         successors successors]
    (if-let [step' (first (successors step))]
      (recur step'
             (conj expansion step')
             (update successors step rest))
      expansion)))
(generate-successors (java.util.Random. 0))
{:start F, :successors {F (+ - - - + + -), - (F F F -), + (F F F)}}

(successors->rule (generate-successors (java.util.Random. 0)))
[F + F - F - F - - F + F + F -]

Looks promising. Let's see what the first handful of seeds generate:

Seed 0, depth 4Seed 1, depth 3Seed 2, depth 6Seed 3, depth 3Seed 4, depth 3Seed 5, depth 3Seed 6, depth 3Seed 7, depth 4Seed 8, depth 3Seed 9, depth 3Seed 10, depth 3Seed 11, depth 3Seed 12, depth 4Seed 13, depth 4Seed 14, depth 3Seed 15, depth 3Seed 16, depth 4Seed 17, depth 5Seed 18, depth 4Seed 19, depth 5Seed 20, depth 3Seed 21, depth 4Seed 22, depth 4Seed 23, depth 3Seed 24, depth 4Seed 25, depth 3Seed 26, depth 3Seed 27, depth 3Seed 28, depth 3Seed 29, depth 4Seed 30, depth 3Seed 31, depth 3

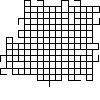
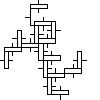
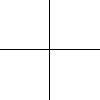
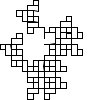
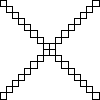
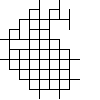
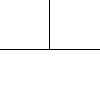
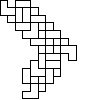
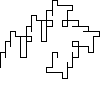
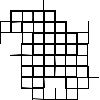
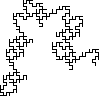
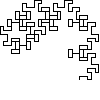
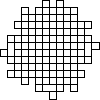
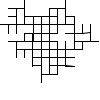
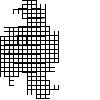
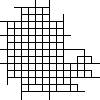
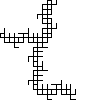
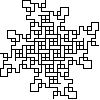
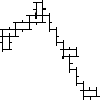
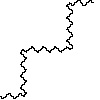
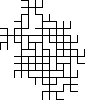
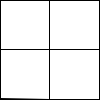
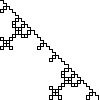
Not all winners, but better than one-in-three.

To improve variety, we can pick different angles:

(defn machine->system-2 [i]
  (let [rng (java.util.Random. i)
        angle (rng-rand-nth rng [30 45 60 90 120 135])]
    {:axiom '[F]
     :rules {'F (successors->rule (generate-successors rng))}
     :moves {'+ [:turn angle]
             '- [:turn angle]
             'F [:forward 1]}}))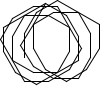
Seed 0, depth 2Seed 1, depth 4Seed 2, depth 3Seed 3, depth 4Seed 4, depth 4Seed 5, depth 3Seed 6, depth 3Seed 7, depth 3Seed 8, depth 3Seed 9, depth 6Seed 10, depth 4Seed 11, depth 5Seed 12, depth 3Seed 13, depth 3Seed 14, depth 3Seed 15, depth 4Seed 16, depth 5Seed 17, depth 4Seed 18, depth 4Seed 19, depth 3Seed 20, depth 2Seed 21, depth 3Seed 22, depth 3Seed 23, depth 3Seed 24, depth 3Seed 25, depth 2Seed 26, depth 3Seed 27, depth 3Seed 28, depth 3Seed 29, depth 3Seed 30, depth 4Seed 31, depth 3

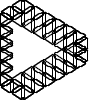
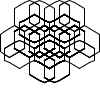
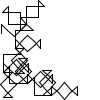
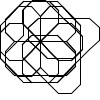
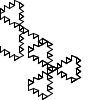
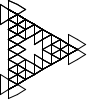
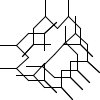
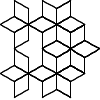
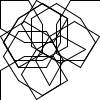
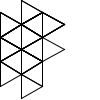
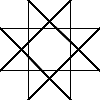
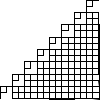
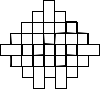
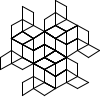
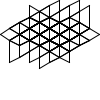
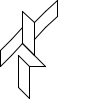
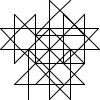
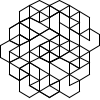
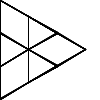
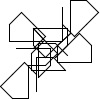
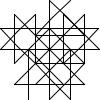
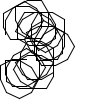
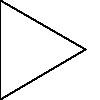
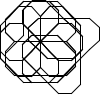
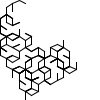
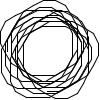
There's a myriad of avenues for further exploration, including two-rule systems, systems that step forward by different distances, systems with more than one turn angle, and combinations of all three. Unfortunately, random generation seems to produce almost exclusively self-intersecting designs, rather than elegant space-filling curves. If we want something like a Hilbert curve or a hexagonal gosper, we probably need to hand-craft it, though some of the random drawings here could serve as inspiration for new designs.