DogBunny puzzle solver
It doesn't seem to be online anymore, but I enjoyed Conrad Barski's DogBunny puzzle. It didn't take more than a couple minutes to solve, and I could usually get within two or three moves of the optimum without trying too desperately. One Wicked Wednesday puzzle, however, did stump me for a while, and though I eventually worked it out, I didn't do so until after I had started writing an automated solver. Here's a walkthrough of the finished solver, using a non-wicked puzzle from several weeks ago.
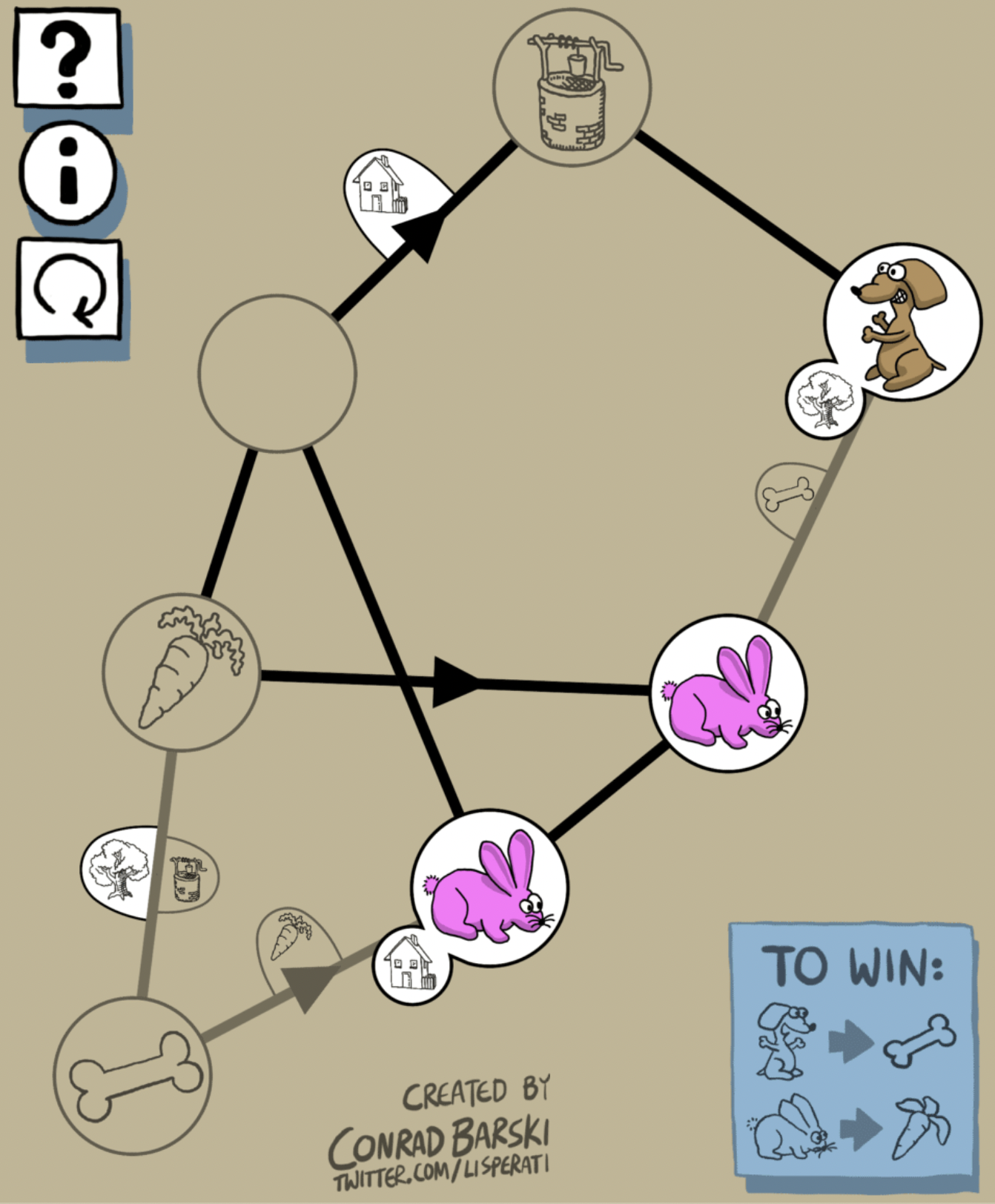
Here are the edges of the puzzle graph:
(def edges
[[:--> :blank-1 :well :house]
[:<-> :well :tree]
[:<-> :blank-1 :carrot]
[:<-> :blank-1 :house]
[:<-> :tree :blank-2 :bone]
[:--> :carrot :blank-2]
[:<-> :carrot :bone (every-pred :tree :well)]
[:<-> :blank-2 :house]
[:--> :bone :house :carrot]]):<-> denotes a bidirectional edge and :--> a unidirectional edge. The optional fourth value in each vector is the condition that must be met for the edge to be traversable. Below we'll collect the names of nodes with animals on them, then put them in a set, so each condition is a function that takes such a set and returns a truthy or falsey value for whether the edge can be walked. Using such a set, we can determine whether a node is occupied using the node's keyword name as a function (as in the first edge, which checks the :house node), or we can use Clojure's higher-order functions to check that a node is empty (using complement, not needed here) or that it meets multiple conditions (using every-pred).
In the absence of specific condition, we'll use constantly to indicate the edge is always traversable:
(def TRUE (constantly true))Our initial state is a map from animals to the nodes on which they start:
(def start-state
{:bunny-1 :house
:bunny-2 :blank-2
:dog :tree})Our goal state is to get the dog to the bone and the bunnies to the carrot:
(def goal-state
{:dog :bone
:bunny-1 :carrot
:bunny-2 :carrot})To simulate playing the game, let's turn our list of edges into a map of maps, structured like this:
{:node-1 {:node-2 :condition-1
:node-3 :condition-2}
:node-2 {:node-1 :condition-1}}This is a common structure for representing graphs. Each node name lists its outbound edges with additional data, in this case just the condition that must be true for the edge to be traversable.
To convert our list edges to such a graph, we can use reduce:
(defn graph [edges]
(reduce
(fn [graph [dir a b pred]]
(let [pred (or pred TRUE)]
(cond-> graph
(#{:--> :<->} dir) (assoc-in [a b] pred)
(#{:<->} dir) (assoc-in [b a] pred))))
{}
edges))(graph edges){:blank-1 {:well :house, :carrot #function[clojure.core/constantly/fn--5740], :house #function[clojure.core/constantly/fn--5740]}, :well {:tree #function[clojure.core/constantly/fn--5740]}, :tree {:well #function[clojure.core/constantly/fn--5740], :blank-2 :bone}, :carrot {:blank-1 #function[clojure.core/constantly/fn--5740], :blank-2 #function[clojure.core/constantly/fn--5740], :bone #function[clojure.core/every-pred/ep2--8679]}, :house {:blank-1 #function[clojure.core/constantly/fn--5740], :blank-2 #function[clojure.core/constantly/fn--5740]}, :blank-2 {:tree :bone, :house #function[clojure.core/constantly/fn--5740]}, :bone {:carrot #function[clojure.core/every-pred/ep2--8679], :house :carrot}}
This graph represents the puzzle as a whole. Given the current locations of the animals, we can remove edges that aren't traversable and simplify the graph to just a map of sets:
(defn current-graph [graph state]
(let [occupied-nodes (set (vals state))]
(into {}
(map (fn [[from-node edges]]
[from-node
(set (keep (fn [[to-node traversable?]]
(when (traversable? occupied-nodes)
to-node))
edges))]))
graph)))(current-graph (graph edges) start-state){:blank-1 #{:well :carrot :house}, :well #{:tree}, :tree #{:well}, :carrot #{:blank-1 :blank-2}, :house #{:blank-1 :blank-2}, :blank-2 #{:house}, :bone #{}}
From this graph of the currently available edges we can list what nodes each animal can move to:
(defn moves [graph state]
(let [graph (current-graph graph state)]
(into #{}
(mapcat (fn [[animal node]]
(map #(do [[animal node] %])
(graph node))))
state)))(moves (graph edges) start-state)#{[[:bunny-2 :blank-2] :house] [[:bunny-1 :house] :blank-1] [[:bunny-1 :house] :blank-2] [[:dog :tree] :well]}
The first value in the vector identifies an animal and the node it's currently on, and the second value names the node to move it to. The animal-node pair is necessary to disambiguate cases where two identical animals are on different nodes but could both move to the same node.
To move an animal to a new node, we update the animal's value in the state map:
(defn move [state [[animal] node]]
(assoc state animal node))(move start-state [[:bunny-1 :bone] :blank-1]){:bunny-1 :blank-1, :bunny-2 :blank-2, :dog :tree}
Now that we can generate different puzzle states, we need a way of exploring those states to reach the solution and return the moves that got us there. The simplest approach is a depth-first search, but on a puzzle like this a depth-first search tends to get stuck going it circles, moving animals back and forth between two nodes until it hits the maximum allowed number of moves, then trying the same thing with two other nodes. Even if a depth-first search does eventually reach the solution, it tends to be very slow getting there.
A faster approach is to create a graph of puzzle states, then walk the shortest path from the starting state to the solution.
The terminology begins to overlap here, due to the DogBunny puzzle being a graph puzzle, but creating a graph of puzzle states can be used for many kinds of puzzles, such as Sudoku or solitaire card games. A graph of puzzle states is a graph where each node is a valid configuration of the puzzle and each edge connects from a valid configuration to another configuration that's reachable in one move.
Given some known states, we can map to all adjacent states like this:
(defn next-states [graph states]
(into {}
(map (fn [state]
[state
(into {}
(map (fn [step]
[step
(move state step)]))
(moves graph state))]))
states))To walk the state graph and build it out, we'll begin with our starting state and find all adjacent states, then for each of the adjacent states find their adjacent states. Any time we reach a state we've already seen, we don't have to walk from it, because we already know what states can be reached from it.
Here's a function to do that, which quits walking when it finds the solution state:
(defn state-graph [graph goal-state start-state]
(loop [new-states #{start-state}
states {}]
(let [solved (filter #(= goal-state %) new-states)]
(cond
(seq solved)
, (with-meta
(into states (map #(do [% {}])) solved)
{:result :solved})
(empty? new-states)
, (with-meta states {:result :finished})
:else
, (let [new-state-graph (next-states graph new-states)
new-states (sequence
(comp
(map val)
(mapcat vals)
(remove states)
(distinct))
new-state-graph)]
(recur new-states
(merge states new-state-graph)))))))Here's a sample of the generated state graph:
(into {}
(take 2)
(state-graph (graph edges) goal-state start-state)){{:bunny-1 :carrot, :bunny-2 :tree, :dog :house} {[[:dog :house] :blank-2] {:bunny-1 :carrot, :bunny-2 :tree, :dog :blank-2}, [[:bunny-1 :carrot] :blank-1] {:bunny-1 :blank-1, :bunny-2 :tree, :dog :house}, [[:dog :house] :blank-1] {:bunny-1 :carrot, :bunny-2 :tree, :dog :blank-1}, [[:bunny-1 :carrot] :blank-2] {:bunny-1 :blank-2, :bunny-2 :tree, :dog :house}, [[:bunny-2 :tree] :well] {:bunny-1 :carrot, :bunny-2 :well, :dog :house}}, {:bunny-1 :blank-1, :bunny-2 :carrot, :dog :blank-1} {[[:dog :blank-1] :carrot] {:bunny-1 :blank-1, :bunny-2 :carrot, :dog :carrot}, [[:dog :blank-1] :house] {:bunny-1 :blank-1, :bunny-2 :carrot, :dog :house}, [[:bunny-2 :carrot] :blank-2] {:bunny-1 :blank-1, :bunny-2 :blank-2, :dog :blank-1}, [[:bunny-1 :blank-1] :house] {:bunny-1 :house, :bunny-2 :carrot, :dog :blank-1}, [[:bunny-1 :blank-1] :carrot] {:bunny-1 :carrot, :bunny-2 :carrot, :dog :blank-1}, [[:bunny-2 :carrot] :blank-1] {:bunny-1 :blank-1, :bunny-2 :blank-1, :dog :blank-1}}}
Each key in the map is a puzzle state, and each value is a map from a move to the puzzle state it results in. We'll use that information below to find the moves that get us from the starting state to the solution, but for now we only care whether we reached a solution or not, which we specified using metadata on the state graph:
(-> (graph edges)
(state-graph goal-state start-state)
meta
:result):solved
The final step is to find the fewest number of moves that take us from the starting state to the solution state. For that, we use Dijkstra's algorithm. The loop re-walks the state graph and collects a map of states and the shortest path to them from our starting state:
(defn shortest-path [state-graph start end]
(loop [new-states #{start}
paths {}]
(or (paths end)
(when-not (empty? new-states)
(let [new-paths (mapcat #(new-paths % state-graph paths)
new-states)]
(recur
(set (map first new-paths))
(into paths new-paths)))))))The core of this logic is in new-paths, which looks up the best path to the current state, and if adding one move to it will be shorter than the best path we already know to the next state, we use that as the new best path to the next state:
(defn new-paths [state state-graph paths]
(map (fn [[move new-state]]
(let [path (paths state [])
best-path (paths new-state)]
(if (and best-path
(< (count best-path)
(inc (count path))))
[new-state best-path]
[new-state (conj path move)])))
(state-graph state)))That gives us the shortest paths from our starting state to the goal state, which allows us to get the solution in an optimal number of moves.
Now we can get the sequence of moves that take us to the starting state to the solution state:
(-> (graph edges)
(state-graph goal-state start-state)
(shortest-path start-state goal-state))[[[:bunny-1 :house] :blank-1] [[:bunny-2 :blank-2] :house] [[:bunny-1 :blank-1] :well] [[:bunny-2 :house] :blank-1] [[:bunny-2 :blank-1] :carrot] [[:bunny-2 :carrot] :bone] [[:dog :tree] :blank-2] [[:dog :blank-2] :house] [[:dog :house] :blank-1] [[:dog :blank-1] :carrot] [[:bunny-2 :bone] :house] [[:dog :carrot] :blank-2] [[:bunny-2 :house] :blank-1] [[:dog :blank-2] :house] [[:bunny-2 :blank-1] :well] [[:dog :house] :blank-1] [[:bunny-1 :well] :tree] [[:dog :blank-1] :carrot] [[:dog :carrot] :bone] [[:bunny-1 :tree] :blank-2] [[:bunny-1 :blank-2] :house] [[:bunny-1 :house] :blank-1] [[:bunny-2 :well] :tree] [[:bunny-2 :tree] :blank-2] [[:bunny-2 :blank-2] :house] [[:bunny-2 :house] :blank-1] [[:bunny-1 :blank-1] :carrot] [[:bunny-2 :blank-1] :carrot]]
This solver is quite fast: on my laptop it solved this 28-step puzzle in about 25 milliseconds.
Note that DogBunny puzzles don't always have a single solution. Often a move can be made with different animals, and moves that are independent of each other can be made in any order.
Compared to solving a DogBunny puzzle manually, this solver's moves often feel disjointed. Rather than making multiple moves in a row to transfer an animal from one node to another, distant node, the solver doesn't mind interspersing unrelated moves of other animals that could have been done equally well after the multi-step transfer. Regardless, it does find optimal solutions that couldn't be any shorter.
If you have a favorite puzzle solver, feel free to show it off and email me.